Комментарии участников:
Почему нет? Они довольно однозначно связаны, поэтому если возможно первое, то вероятно и второе. Разрывы производной смущают, конечно.
Просто форма явно для этой системы больше подходит, скорее всего запись даже проще выглядела бы.
Просто форма явно для этой системы больше подходит, скорее всего запись даже проще выглядела бы.
Как мне кажется, в декартовой системе каждый участок этого Бэтмена задаётся довольно просто, но я не представляю, как можно так же просто задать его в полярной системе. Как, например, будет выглядеть в ней обычная квадратичная функция?
Нифига, поскольку формула вида x*y*z=0, то каждый сомножитель должен давать чёткий кусок в своей области определения.
хммм, видимо вы правы. присмотрелся повнимательнее, первая скобка — кусок элипса (внешние части «крыла») — он(они) вполне просмотривается на графике
Ну, в общем почти так и есть.
Функции двух переменных геогебра умеет только линейные и квадратичные, поэтому с первой скобкой ничего не получилось, но поверим на слово, и так видно.
Картинка в теме формуле немного не соответствует, форма та же, а вот абсолютные значения не те, но не столь важно. Вторая скобка с нижним краем хороша.
линк
Функции двух переменных геогебра умеет только линейные и квадратичные, поэтому с первой скобкой ничего не получилось, но поверим на слово, и так видно.
Картинка в теме формуле немного не соответствует, форма та же, а вот абсолютные значения не те, но не столь важно. Вторая скобка с нижним краем хороша.
линкКартинка в теме формуле немного не соответствуеттам шкала епнутая. присмотритесь.
параметры первого элипса — 3, 7 вполне четко видны. и область определения первой скобки — модуль икс больше трех — тоже видны.
Что вы хотите, оно изначально кривое. Кто видел мышей с эллипсовидными крыльями?
Наша грушная мыша правдоподобней.
источник: img.likeness.ru
Наша грушная мыша правдоподобней.
источник: img.likeness.ru
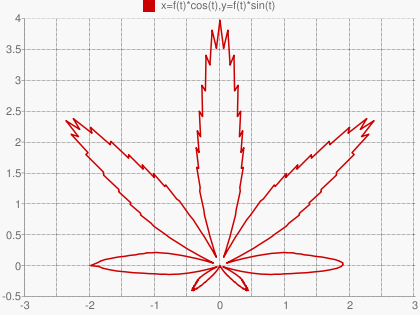
Есть еще старая добрая каннабиоида.
f=func('t','(1+sin(t))*(1+0.9*cos(8*t))*(1+0.1*cos(24*t))*(0.9+0.05*cos(200*t))'); parplot(['f(t)*cos(t)','f(t)*sin(t)'],[-pi,pi],[-3,3],[-0.5,4])
источник: live.mephist.ru
f=func('t','(1+sin(t))*(1+0.9*cos(8*t))*(1+0.1*cos(24*t))*(0.9+0.05*cos(200*t))'); parplot(['f(t)*cos(t)','f(t)*sin(t)'],[-pi,pi],[-3,3],[-0.5,4])
источник: live.mephist.ru
Мне просто интересно, смотря на эти ФОрмулы я один таким тупым себя ощущаю? Или на н2 все физмат заканчивали?
это же элементарная вышка ) проходят по-моему все на 1-2 курсах… хотя насчёт гуманитариев не уверен.
Гуманитарии тоже проходят, на 1 курсе, далеком аки торжество демократии в России. Но дело в том Как на эту формула и график смотрят ребята закончившие гум.фак и мат.-физ.фак. У меня одно с другим не особо соотносится. А про полярную систему координат я узнал только щас от своего соседа — выпускника СУНЦа.))
