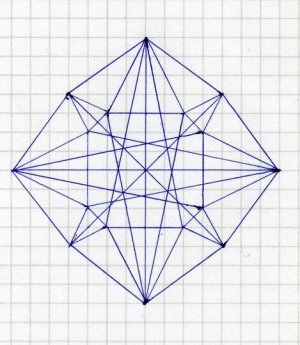
Почему объёмная геометрия вышла за пределы учебника?

Объёмные многогранники давно покинули страницы школьных задачников и перебрались в арт-студии, альбомы урбан-скетчеров и цифровые игры. «Додекаэдр манит симметрией, но остаётся дружелюбным для новичка, если разложить его на сетку» — отмечает преподаватель черчения Вера Кузьмина. А сетка в клетку делает процесс настолько простым, что превращает классическую геометрию в расслабляющее творчество.

Что такое додекаэдр и чем он интересен художнику

Додекаэдр состоит из двенадцати равных пятиугольников. Его форма встречается в кристаллах граната и архитектуре Бакинского Центра Гейдара Алиева. Для рисовальщика это тренажёр перспективы, света и тени.

Главные плюсы

• Простая логика построения — достаточно один раз понять шаг, чтобы повторять фигуру с любым масштабом

• Возможность тренировать штрих и градации серого на каждой грани

• Эффектный результат — рисунок выглядит сложным, хотя строится по ясному алгоритму

Материалы без лишних затрат

• Лист бумаги с крупной или средней клеткой
• Простой карандаш HB и ластик
• Чёрный лайнер 0,3 мм для контура
• Серый маркер или мягкий графит 2B для теней
• Линейка, если клетки слишком мелкие

Подготовка сетки, чтобы не сбиться

Отметьте на листе квадрат шестнадцать на шестнадцать клеток. Внутри него поместится полный разворот додекаэдра, а запасные клетки по краям защитят от срезанных граней.

Шаговый алгоритм построения

Шаг первый — базовый пятиугольник

Найдите центр сетки, вокруг него постройте равносторонний пятиугольник сторонами по четыре клетки.

Шаг второй — добавляем глубину

От каждой стороны проводите внутрь диагональ длиной две клетки, так возникают наклонные рёбра.

Шаг третий — формируем соседние грани

Используя диагонали как основание, достройте ещё пять пятиугольников. Следите за тем, чтобы их стороны также равнялись четырём клеткам.

Шаг четвёртый — замыкаем верхнюю и нижнюю часть

Соедините вершины соседних граней и получите четырёхугольные проекции, которые станут рёбрами верхней и нижней «шапки».

Шаг пятый — уточняем контур

Лайнером обведите только видимые рёбра. Стержнем карандаша уберите строительные линии, оставив чистую геометрию.

Шаг шестой — свет и тень

Выберите источник света сверху слева. Легче всего разделить грани на три тона, светлый, средний, тёмный. «Контраст в три ступени создаёт убедительную объёмность без перегруза деталями» — советует иллюстратор Павел Юдин.

Как усложнить задачу и сделать рисунок уникальным

• Раскрасьте каждую грань отдельным цветом, получите эффект кристалла

• Добавьте узор в пятиугольники, например славянский орнамент или пиксельный градиент

• Попробуйте зеркальное отражение фигуры в условной воде, тренируя симметрию и обратную перспективу

• Переведите рисунок в цифровой редактор, замените линии на светящиеся неон-эффекты

Типичные ошибки и их быстрое лечение

Ошибка Пятиугольники распухли и утратили равенство

Решение Вернитесь к сетке, проверяйте длину сторон по клеткам, не доверяйте на глаз

Ошибка Тени хаотичны, объём исчез

Решение Перед затенением сделайте лёгкий план-схему штриховки карандашом, лишь потом наносите плотный тон

Ошибка Контур дрожит

Решение Ведите лайнер по линейке, но ставьте её чуть в стороне, чтобы чернила не затекали под пластик

Чек-лист перед публикацией

• Все видимые рёбра прямые, невидимые не выбиваются наружу
• Грани поделены на три тона, свет направлен из одной точки
• Нет случайных пятен ластика или грязных следов
• Фото сделано при нейтральном дневном освещении, сетка читается

Таким образом додекаэдр по клеточкам превращается из пугающей учебной модели в увлекательный квест, где каждая запланированная клетка приносит чувство контроля, а итоговый объём дарит эффект «вау». От первого пятиугольника до последней тени — весь путь занимает не больше часа, но за это время рука привыкает к точности, а глаз к гармонии. Попробуйте построить собственный многогранник уже сегодня и убедитесь, что сложная геометрия покоряется простым квадратикам.